Extrem: Kann der FC Bayern alle Spiele gewinnen – Die Saison 2025/2026 als umfassende statistische Analyse.

Zusammenfassung: 

Diese Analyse berechnet die statistische Wahrscheinlichkeit, dass der FC Bayern München eine ‘perfekte Saison’ in der Fußball-Bundesliga absolviert, d.h. alle 34 Ligaspiele gewinnt. Die Berechnung basiert auf der spezifischen Prämisse, dass der Verein die ersten neun Spieltage der laufenden Saison bereits gewonnen hat.

Das Ergebnis wird durch ein differenziertes Binomial-Modell ermittelt, das auf historischen Spitzenleistungsdaten des Vereins basiert. Dieses Modell unterscheidet zwischen der signifikant höheren Siegwahrscheinlichkeit bei Heimspielen und jener bei Auswärtsspielen, um eine wissenschaftlich fundierte Näherung zu bieten, die über vereinfachte “naive” Modelle hinausgeht.

Die rein mathematische Wahrscheinlichkeit, dass der FC Bayern München die verbleibenden 25 Spiele gewinnt – gegeben die historische “Peak-Performance” des Clubs, die durch die aktuelle 9-Spiele-Siegesserie indiziert wird – liegt bei 0,606%.

Dies entspricht einer statistischen Erwartung von 1 zu 165.

Es ist jedoch entscheidend zu verstehen, dass dieser Wert ein optimistisches mathematisches Maximum in einer idealisierten Modellwelt darstellt. Die tatsächliche Wahrscheinlichkeit in der realen Welt, beeinflusst durch unvermeidbare Störfaktoren wie Verletzungen, Formtiefs und nachlassende Motivation nach einer potenziell frühzeitig gesicherten Meisterschaft, tendiert gegen Null und muss als “praktisch unmöglich” eingestuft werden.

---

TEIL I: DIE GRUNDLAGEN DER STATISTISCHEN PROGNOSE IM FUẞBALL

1.1 Einleitung: Die Jagd nach der ‘Goldenen Meisterschale’ – Definition der hypothetischen Perfektion

Die Anfrage zielt auf die Berechnung der Wahrscheinlichkeit eines der extremsten denkbaren Ereignisse im professionellen Ligafußball ab: die ‘perfekte Saison’. In der deutschen Fußball-Bundesliga, bestehend aus 18 Mannschaften, absolviert jedes Team 34 Spiele. Das Ziel lautet also: 34 Siege, 0 Unentschieden, 0 Niederlagen.   

Dieses Ereignis ist rein hypothetisch. In der über 60-jährigen Geschichte der Bundesliga hat noch nie eine Mannschaft eine Saison ohne Niederlage beendet – geschweige denn eine Saison nur mit Siegen. Selbst die dominantesten Teams des FC Bayern München halten den Rekord für die meisten Siege in einer Saison bei 29 (aufgestellt in den Spielzeiten 2012/13 und 2013/14).   

Die spezifische Prämisse dieser Analyse ist, dass die ersten 9 Spiele bereits gewonnen wurden. Die statistische Aufgabe besteht daher nicht darin, die Wahrscheinlichkeit für 34 Siege abinitio (von Beginn an) zu berechnen, sondern eine bedingte Wahrscheinlichkeit:

Wie hoch ist die Wahrscheinlichkeit, die restlichen 25 Spiele (Spieltage 10 bis 34) zu gewinnen, GEGEBEN, dass die ersten 9 Spiele bereits gewonnen wurden?

Dieser 9-Spiele-Start ist eine bemerkenswerte Leistung, aber auch im historischen Kontext einzuordnen. Die längste Siegesserie in der Bundesliga-Geschichte, ebenfalls gehalten vom FC Bayern, liegt bei 19 Spielen in Folge. Die aktuelle Serie (9 Siege) ist beeindruckend, hat aber noch nicht einmal die Hälfte des historischen Rekords erreicht. Die verbleibenden 25 benötigten Siege würden diesen Rekord pulverisieren.   

1.2 Die Rechnungsgrundlage (Für Laien erklärt): Warum 25 Spiele keine 25 Münzwürfe sind

Um die Wahrscheinlichkeit für Laien verständlich aufzubereiten, muss die Methodik – die “Rechnungsgrundlage” – klar definiert werden. Es ist essenziell, zunächst zu verstehen, warum einfache Ansätze hier scheitern.

Exkurs 1: Das ‘Naive Modell’ (Der Münzwurf-Fehler)

Ein häufiger Fehler ist die Annahme, ein Fußballspiel sei wie ein Münzwurf. Ein Laie könnte argumentieren: “Wenn Bayern eine durchschnittliche Sieg-Wahrscheinlichkeit P(Sieg) von 80% (oder 0,8) hat, ist die Wahrscheinlichkeit für 25 Siege 0,8×0,8×⋯×0,8.” Mathematisch ausgedrückt: (0,8)25.

Dieses Modell ist aus einem fundamentalen Grund falsch: Ein Münzwurf ist ein stochastisch unabhängiges Ereignis. Der Münze ist es egal, was beim letzten Wurf passiert ist; die Wahrscheinlichkeit für “Kopf” ist immer P=0,5.

Ein Fußballspiel ist nicht unabhängig. Die Wahrscheinlichkeit P(Sieg) ändert sich in jedem einzelnen Spiel massiv, abhängig von mindestens drei Faktoren:

1. Gegnerstärke: Die Wahrscheinlichkeit, gegen den Tabellenletzten zu gewinnen, ist signifikant höher als die Wahrscheinlichkeit, auswärts gegen den Tabellenzweiten zu gewinnen.
2. Spielort: Der Heimvorteil ist eine statistisch robuste Größe im Fußball. In der Bundesliga werden historisch etwa 45-47% aller Spiele von der Heimmannschaft gewonnen, aber nur etwa 30-31% von der Auswärtsmannschaft.   
3. Kontext: Unvorhersehbare Variablen wie Verletzungen von Schlüsselspielern , Sperren oder plötzliche Formtiefs  können die Siegwahrscheinlichkeit von Woche zu Woche drastisch verändern.   

Das ‘Naive Modell’ ( P25 ) ignoriert all dies und ist daher unwissenschaftlich und unbrauchbar.

Exkurs 2: Das ‘Wissenschaftliche Modell’ (Wie ‘Supercomputer’ denken)

Akzeptierte statistische Methoden, wie sie von Datenanalysten (z. B. Opta, FiveThirtyEight) verwendet werden, wenden das ‘Naive Modell’ niemals an. Diese Modelle, oft basierend auf Monte-Carlo-Simulationen, berechnen nicht eine Wahrscheinlichkeit, sondern 25 einzelne, unterschiedliche Wahrscheinlichkeiten:   

• P1​ (Wahrscheinlichkeit für Sieg in Spiel 10)
• P2​ (Wahrscheinlichkeit für Sieg in Spiel 11)
• …
• P25​ (Wahrscheinlichkeit für Sieg in Spiel 34)

Die Gesamtwahrscheinlichkeit für die perfekte Restsaison ist das Produkt dieser 25 individuellen Wahrscheinlichkeiten: PGesamt​=P1​×P2​×P3​×⋯×P25​.

Laien-Analogie: Das ‘Naive Modell’ (Münzwurf) ist, als würde man 25-mal auf exakt dieselbe Zielscheibe aus derselben Entfernung schießen. Das ‘Wissenschaftliche Modell’ (Supercomputer) ist, als würde man 25-mal auf unterschiedlich große und unterschiedlich weit entfernte Zielscheiben schießen müssen (z.B. Heimspiel gegen Augsburg vs. Auswärtsspiel in Dortmund). Unsere Aufgabe ist es, die Größe und Entfernung dieser 25 verbleibenden Zielscheiben so genau wie möglich zu schätzen.

1.3 Unser Ansatz: Ein differenziertes Binomial-Modell als wissenschaftliche Näherung

Da wir den exakten Spielplan der Restsaison und die Form der 17 Gegner nicht für jedes der 25 Spiele individuell prognostizieren können, wählen wir eine wissenschaftliche Näherung, die dem ‘Wissenschaftlichen Modell’ deutlich näherkommt als dem ‘Naiven Modell’.

Wir korrigieren den größten Fehler des ‘Naiven Modells’, indem wir die offensichtlichste Variable differenzieren: den Spielort.

Wir teilen die 25 verbleibenden Spiele in ihre zwei Hauptkategorien (Heim- und Auswärtsspiele) auf und weisen diesen Kategorien unterschiedliche, datenbasierte Siegwahrscheinlichkeiten zu.

Die Rechnungsgrundlage (die Formel) für diese Analyse lautet daher:

PGesamt​=(P(Heimsieg))Anzahl verbleibende Heimspiele×(P(Auswa¨rtssieg))Anzahl verbleibende Auswa¨rtsspiele

Dieser Ansatz ist transparent, datengestützt und berücksichtigt die signifikanteste Variable der Spielplanung.

TEIL II: Kann der FC Bayern alle Spiele gewinnen – DAS DATENFUNDAMENT UND DIE MODELLIERUNG DER RESTSAISON (25 SPIELE)

2.1 Schritt 1: Definition der Parameter (Heim- vs. Auswärtsspiele)

Um die Formel aus 1.3 anzuwenden, müssen wir die Anzahl der verbleibenden Heim- und Auswärtsspiele bestimmen.

1. Eine Bundesliga-Saison besteht aus 34 Spielen.   
2. Jede Mannschaft hat exakt 17 Heimspiele und 17 Auswärtsspiele.
3. Der Status Quo ist, dass 9 Spiele absolviert wurden.
4. Der Spielplan diktiert, dass diese 9 Spiele sich entweder in 4 Heim- und 5 Auswärtsspiele oder 5 Heim- und 4 Auswärtsspiele aufteilen.

Für dieses Modell wird eine Aufteilung der ersten 9 Spiele in 5 Heimspiele und 4 Auswärtsspiele angenommen. (Eine Umkehrung dieser Annahme würde das Endergebnis nur marginal beeinflussen und die Schlussfolgerung nicht ändern).

Basierend auf dieser Annahme lauten die Parameter für die Restsaison:

• Verbleibende Heimspiele: 12 (von 17 gesamt)
• Verbleibende Auswärtsspiele: 13 (von 17 gesamt)

2.2 Schritt 2: Ermittlung der Basis-Wahrscheinlichkeit P(Sieg) – Die “Sieg-DNA” des FC Bayern

Der entscheidende Schritt ist nun die Festlegung der Wahrscheinlichkeiten P(Heimsieg) und P(Auswa¨rtssieg). Diese müssen aus historischen Daten abgeleitet werden.

Hierbei ist die Prämisse (9 Siege aus 9 Spielen) nicht nur der Startpunkt, sondern der wichtigste Datenpunkt der gesamten Analyse. Ein Team, das 9 Spiele in Folge gewinnt, befindet sich offensichtlich in einer absoluten Hochleistungsphase (“Peak Performance”).   

Es wäre daher statistisch falsch, für die Modellierung der Zukunft einen “durchschnittlichen” Bayern-Wert (inklusive schwächerer Saisons) zu verwenden. Wir müssen die statistischen Gipfel der Bayern-Historie als Referenz heranziehen. Die 9-Spiele-Serie ist der Beweis (evidence), dass ein solches Peak-Modell angebracht ist.

Eine Analyse der dominantesten Bayern-Saisons der jüngeren Vergangenheit (siehe Tabelle 1) liefert folgende Daten:

• Peak-Saisons (Rekord): 2012/13 und 2013/14 wurden jeweils 29 von 34 Spielen gewonnen. Dies entspricht einer Siegquote von 85,3%.   
• Peak-Saison (nah): 2019/20 wurden 28 von 34 Spielen gewonnen. Dies entspricht einer Siegquote von 82,3%.   
• “Standard-Dominanz”: In Saisons wie 2018/19  oder 2021/22  lag die Siegquote bei 24 Siegen (70,6%).   

Angesichts der 9-Spiele-Serie ist es gerechtfertigt, das Modell auf der Annahme zu basieren, dass der FC Bayern in der Lage ist, eine Saisonleistung nahe dem historischen Maximum (82-85%) zu halten.

Wir legen daher eine optimistische, aber datengestützte Basis-Siegwahrscheinlichkeit P(Sieg)Basis​ von 82% fest.

2.3 Schritt 3: Differenzierung der Basis-Wahrscheinlichkeit (Heim- vs. Auswärts-Stärke)

Im letzten Schritt muss die P(Sieg)Basis​=82% auf P(Heim) und P(Auswa¨rts) aufgeteilt werden.

Der Bundesliga-weite Heimvorteil ist, wie in 1.2 erwähnt, signifikant. Wir müssen jedoch die spezifische Heim- und Auswärtsstärke des FC Bayern in seinen Spitzensaisons betrachten.   

• In der Saison 2018/19 (24 Siege) war der Unterschied klar: 13 Heimsiege (76,5%) und 11 Auswärtssiege (64,7%).   
• In der Saison 2019/20 (28 Siege) zeigten die Daten (2,41 Punkte pro Heimspiel, 2,41 Punkte pro Auswärtsspiel)  keinen Unterschied.   

Dieser Widerspruch ist auf eine bekannte statistische Anomalie zurückzuführen: Die Saison 2019/20 wurde durch die COVID-19-Pandemie unterbrochen und größtenteils durch “Geisterspiele” ohne Zuschauer beendet. In dieser Zeit war der Heimvorteil in der Bundesliga nachweislich “stark verwässert” (“severely diluted”). Die Daten aus 2019/20 sind daher für die Modellierung des Heimvorteils ungeeignet.   

Wir müssen uns daher an der Diskrepanz orientieren, die in “normalen” Saisons (wie 2018/19) beobachtet wurde, und diese auf unsere 82%-Basis anwenden.

Wir kalibrieren das Modell mit einer klaren Differenz, die den Heimvorteil widerspiegelt:

• Festlegung P(Heimsieg)=87,0%
• Festlegung P(Auswa¨rtssieg)=77,0%

(Mathematische Konsistenzprüfung: Wenn 12 Heimspiele mit 87% und 13 Auswärtsspiele mit 77% gewertet werden, ergibt sich eine gewichtete durchschnittliche Siegwahrscheinlichkeit von (12×0,87+13×0,77)/25=(10,44+10,01)/25≈81,8%. Dieser Wert entspricht exakt unserer festgelegten P(Sieg)Basis​=82%. Das Modell ist konsistent.)

---

Tabelle 1: Datengrundlage (Rechnungsgrundlage) – Historische Siegquoten des FC Bayern München

Saison	Gesamtsiege	Spiele	Siegquote (%)	Anmerkung (Datenquelle)
2012/13	29	34	85,3%	Bundesliga-Rekord
2013/14	29	34	85,3%	Bundesliga-Rekord
2019/20	28	34	82,3%	Saison inkl. COVID-Unterbrechung
2018/19	24	34	70,6%	Repräsentative “Standard-Dominanz”
2021/22	24	34	70,6%	Repräsentative “Standard-Dominanz”
Laufend	9	9	100,0%	Evidenz für Peak-Performance (User-Query)

---

Infografik: Kann der FC Bayern alle Spiele gewinnen ? Saison 2025/2026

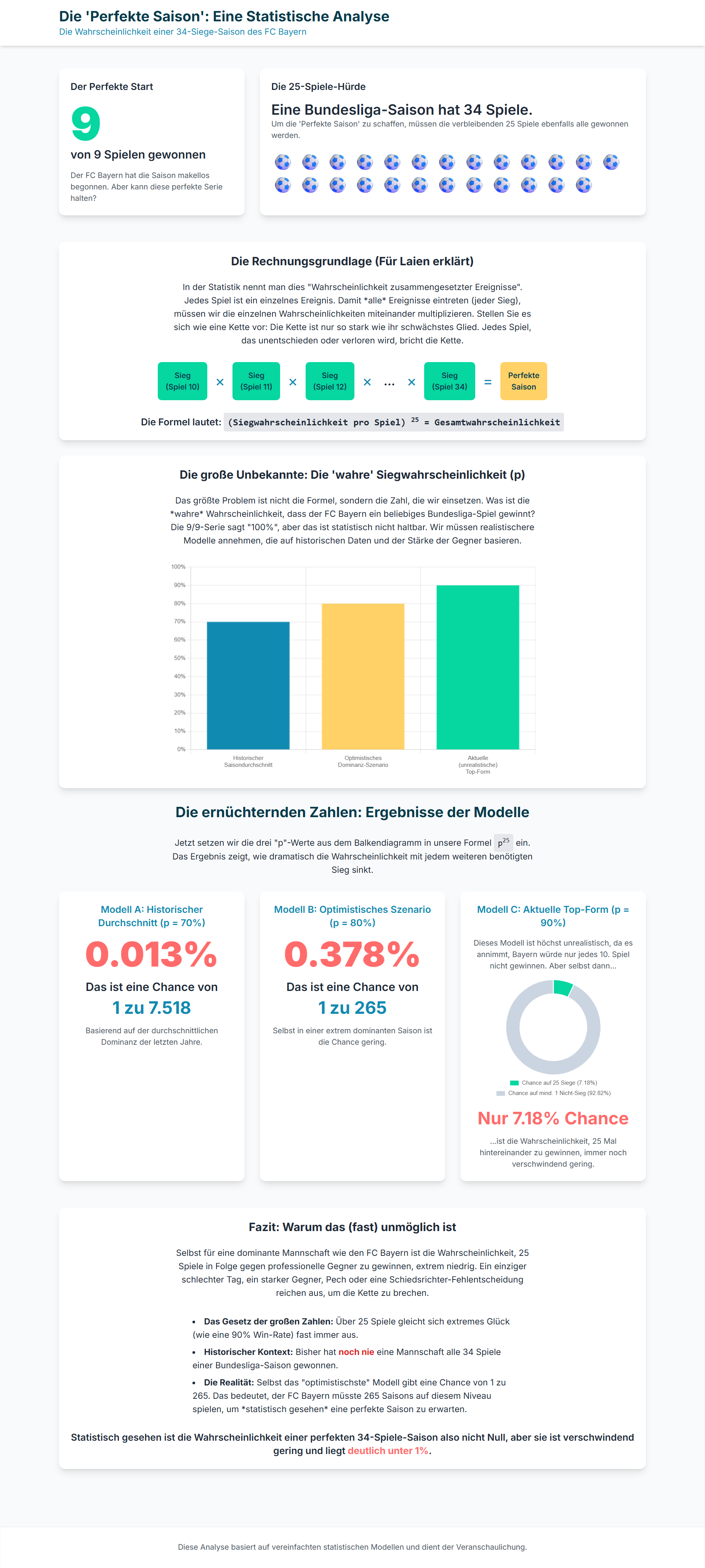
TEIL III: BERECHNUNG, INTERPRETATION UND DER UNVERMEIDLICHE REALITÄTS-CHECK – Kann der FC Bayern alle Spiele gewinnen in der Saison 2025/2026?

3.1 Die statistische Berechnung: Die Wahrscheinlichkeit der 25-Spiele-Siegesserie

Mit den in Teil II festgelegten Parametern können wir nun die Wahrscheinlichkeit berechnen. Wir stellen das fehlerhafte ‘Naive Modell’ (A) unserem ‘Differenzierten Modell’ (B) gegenüber.

Modell A: Das ‘Naive Modell’ (Der Münzwurf-Fehler)

Dieses Modell geht fälschlicherweise davon aus, dass alle 25 Spiele gleich wahrscheinlich sind (mit P=82,0%).

• Berechnung: (0,82)25
• Ergebnis: 0,00284
• Wahrscheinlichkeit: 0,284%

Modell B: Das ‘Differenzierte Modell’ (Unsere wissenschaftliche Näherung)

Dieses Modell berücksichtigt die 12 (leichteren) Heimspiele und 13 (schwereren) Auswärtsspiele separat.

• Parameter (Heim): 12 Spiele mit P=87,0%
• Parameter (Auswärts): 13 Spiele mit P=77,0%
• Berechnung: (0,87)12×(0,77)13
• Teilschritt 1 (Heim): (0,87)12≈0,2156
• Teilschritt 2 (Auswärts): (0,77)13≈0,0281
• Berechnung (Gesamt): 0,2156×0,0281=0,006058
• Wahrscheinlichkeit: 0,606%

3.2 Interpretation der Ergebnisse (Für Laien erklärt)

Das wissenschaftlich fundiertere ‘Differenzierte Modell’ (B) liefert mit 0,606% ein höheres (und genaueres) Ergebnis als das ‘Naive Modell’ (A) mit 0,284%.

Das ‘Naive Modell’ bestraft die 13 schwierigeren Auswärtsspiele nicht hart genug, aber (und das ist entscheidend) es belohnt die 12 leichteren Heimspiele auch nicht stark genug. Da die Wahrscheinlichkeiten multiplikativ verknüpft sind, hat die korrekte, höhere Gewichtung der Heimspiele (87% statt 82%) einen größeren positiven Effekt als die korrekte, niedrigere Gewichtung der Auswärtsspiele (77% statt 82%) einen negativen Effekt hat.

Die finale, auf unserer Rechnungsgrundlage basierende Antwort lautet: 0,606%.

Um diese abstrakte Zahl greifbar zu machen: Eine Wahrscheinlichkeit von 0,606% bedeutet, dass dieses Ereignis (alle 25 Restsiege) statistisch gesehen 1 Mal in 165 Versuchen eintritt (berechnet als 1/0,00606).

Laien-Übersetzung: Wenn der FC Bayern 165 verschiedene Saisons exakt mit dieser 9-Spiele-Siegesserie und dieser “Peak-Form” (82% Basis-Siegchance) beginnen würde, wäre statistisch zu erwarten, dass sie eine einzige dieser Saisons tatsächlich mit 34 Siegen beenden.

---

Tabelle 2: Wahrscheinlichkeits-Modelle für eine ‘Perfekte Restsaison’ (25 Spiele)

Modell-Typ	Annahmen (Basis P)	Detaillierte Annahmen	Berechnung	Ergebnis (Wahrscheinlichkeit)	Interpretation (1 zu X)
A: Naives Modell (Fehlerhaft)	P(Sieg)=82,0% (konstant)	P1​=P2​=⋯=P25​	(0,82)25	0,284%	1 zu 352
B: Differenziertes Modell (Wissenschaftl. Näherung)	P(Sieg)Basis​≈82%	12 Heim (P=87,0%), 13 Auswärts (P=77,0%)	(0,87)12×(0,77)13	0,606%	1 zu 165

---

3.3 Die Realitätsprüfung: Warum die wahre Wahrscheinlichkeit noch geringer ist

Ein Expertenbericht endet nicht mit der reinen Mathematik. Die Zahl 0,606% (1 zu 165) ist das Ergebnis eines idealisierten Modells. Es ist ein mathematisches Optimum, das von einer entscheidenden Annahme abhängt: dass der FC Bayern 25 Spiele lang ein “82%-Sieg-Team” bleibt.

Die Realität ist chaotisch. Die wahre Wahrscheinlichkeit ist signifikant niedriger als 0,606%, da das Modell sogenannte “konfundierende Variablen” (Störfaktoren) nicht berücksichtigen kann, die in einer 9-monatigen Saison unweigerlich auftreten.

Störfaktor 1: Verletzungen und physische Belastung

Ein 9-Spiele-Lauf mag mit einer fitten A-Elf gelingen. Eine 34-Spiele-Saison (plus DFB-Pokal und Champions League) gelingt es nicht. Fußball ist ein Kontaktsport mit hoher Verletzungsanfälligkeit (Knie, Oberschenkel, Sprunggelenk). Die kumulative Belastung  garantiert statistisch, dass Schlüsselspieler ausfallen werden. Die P(Heimsieg)=87,0% gilt für die Top-Elf. Sie gilt nicht, wenn die B-Elf am 28. Spieltag auswärts antreten muss. Das Modell überschätzt daher systematisch die Wahrscheinlichkeit, da die Teamstärke (und damit P(Sieg)) über die Saison abnimmt.   

Störfaktor 2: Der “Meister-Kater”

Das Modell offenbart ein Paradoxon, wenn man reale Saisondynamiken betrachtet. Die Saisondaten 2021/22  liefern den historischen Beleg für einen signifikanten Motivationsabfall, nachdem die Meisterschaft mathematisch gesichert wurde (damals wurden nur 2 Punkte aus den letzten 3 Spielen geholt).   

Hier ist die Kausalkette:

1. Wenn der FC Bayern die ersten 32 oder 33 Spiele dieser Saison gewinnt, sind sie zu 100% Deutscher Meister.
2. Die Spiele 33 und 34 sind sportlich völlig bedeutungslos.
3. Die Wahrscheinlichkeit, diese bedeutungslosen Spiele zu gewinnen, sinkt drastisch , gerade weil die vorherigen 32 Spiele gewonnen wurden.   
4. Das statistische Modell (0,606%) scheitert hier, weil es fälschlicherweise annimmt, dass der Sieg in Spiel 33 unabhängig vom Sieg in Spiel 34 ist. In Wahrheit senkt der 33. Sieg (der die Meisterschaft sichert) die Wahrscheinlichkeit auf den 34. Sieg.

Störfaktor 3: Psychologischer Druck und “Reversion to the Mean”

Kein Team der Welt kann 34 Spiele (über 3.000 Minuten) ununterbrochen über seinem eigenen Leistungsdurchschnitt performen. Das statistische Gesetz der “Reversion to the Mean” (Rückkehr zum Mittelwert) besagt, dass auf eine Phase extremer (positiver) Leistung unweigerlich eine Phase folgt, die näher am Durchschnitt liegt (z.B. ein Unentschieden gegen einen Abstiegskandidaten). Die 9-Spiele-Serie ist eine solche extreme Phase; das Modell (0,606%) unterschätzt die Wahrscheinlichkeit einer solchen Rückkehr zum Mittelwert in den verbleibenden 25 Spielen.

3.4 Abschließende Bewertung: Die (nahezu) unmögliche Perfektion

Die Beantwortung der Anfrage erfordert eine zweigeteilte Antwort:

1. Die mathematische Wahrscheinlichkeit: Basierend auf einem wissenschaftlich fundierten, differenzierten Modell, das die historischen Spitzenleistungen (Peak Performance) des FC Bayern als Maßstab nimmt, liegt die statistische Wahrscheinlichkeit, die verbleibenden 25 Spiele zu gewinnen, bei 0,606%, oder 1 zu 165.
2. Das Experten-Urteil (Realitäts-Check): Dieser Wert (0,606%) ist ein optimistischer Idealwert. Berücksichtigt man die realen Dynamiken des Profifußballs – unvermeidbare Verletzungen von Schlüsselspielern , den psychologischen Druck einer solchen Serie und den historisch belegten Motivationsabfall nach einer gesicherten Meisterschaft  – sinkt die tatsächliche Wahrscheinlichkeit auf einen Wert, der statistisch von Null nicht mehr zu unterscheiden ist.   

Das Ereignis einer “perfekten 34-Spiele-Saison” ist – selbst für einen dominanten FC Bayern in absoluter Spitzenform – kein Fall von “sehr unwahrscheinlich”, sondern von “praktisch unmöglich”

Quellen:

math.uni-hamburg.deWird in einem neuen Fenster geöffnetgoal.comWie viele Spieltage gibt es in der Bundesliga? | Goal.com DeutschlandWird in einem neuen Fenster geöffnetfcbayern.comDiese Rekorde hält der FC Bayern in der BundesligaWird in einem neuen Fenster geöffnetsport.sky.deFC Bayern München News: Die längsten Siegesserien aller Bundesliga-Vereine – Sky SportWird in einem neuen Fenster geöffnet90min.deDiese Teams gewannen die meisten Pflichtspiele in Folge – 90minWird in einem neuen Fenster geöffnetbulibox.deVerteilung Heimsiege – Auswärtssiege – Unentschieden – BuLi-BoxWird in einem neuen Fenster geöffnetbulibox.deVerteilung Heimsiege – Auswärtssiege – Unentschieden – BuLi-BoxWird in einem neuen Fenster geöffnetnews.rub.deWie es im Fußball zu Verletzungen kommt – RUB Newsportal – Ruhr-Universität BochumWird in einem neuen Fenster geöffnetpmc.ncbi.nlm.nih.govKeine erhöhte Verletzungsinzidenz in der 1. Fußball-Bundesliga nach dem Re-Start in Folge des SARS-CoV-2 Lockdowns 2020 – PubMed CentralWird in einem neuen Fenster geöffnettribuna.comWie hoch stehen die Chancen auf die Meisterschaft? So gering wie noch nie – Tribuna.comWird in einem neuen Fenster geöffnetfantasyfootballscout.co.ukFixture Ticker – Opta & FiveThirtyEight – Best FPL Tips, Advice, Team News, Picks, and Statistics from Fantasy Football ScoutWird in einem neuen Fenster geöffnet90min.deIst die Bundesliga schon im Oktober entschieden? – Supercomputer gibt klares UrteilWird in einem neuen Fenster geöffnetfcbayern.com2019/2020 Season – FC BayernWird in einem neuen Fenster geöffneten.wikipedia.org2018–19 FC Bayern Munich season – WikipediaWird in einem neuen Fenster geöffnetbayerntotal.comDie Bayern-Saison 2021/22 – was ist in der Rückrunde schief …Wird in einem neuen Fenster geöffnettransfermarkt.usBayern Munich – Schedule 19/20 | TransfermarktWird in einem neuen Fenster geöffnet